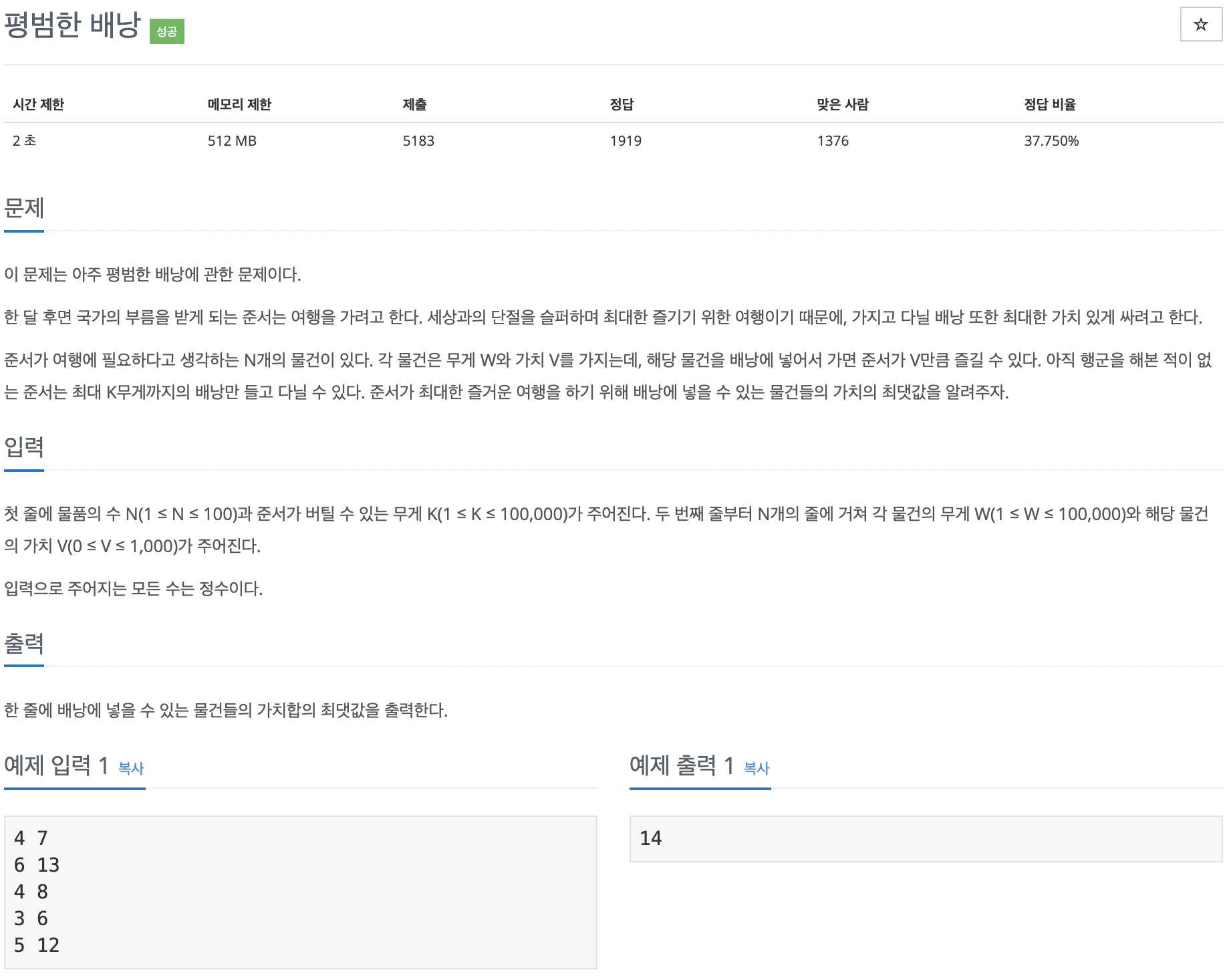
https://www.acmicpc.net/problem/12865
#Solution
https://huiyu.tistory.com/entry/DP-01-Knapsack%EB%B0%B0%EB%82%AD-%EB%AC%B8%EC%A0%9C 참조하였음.
유명한 냅색 문제, 냅색 알고리즘이다.
간단하게 말하면, 한 도둑이 훔치는 배낭에 담을 수 있는 무게의 최댓값이 정해져 있고, 일정 가치와 무게가 있는 짐들을 배낭에 넣을 때, 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제이다.

냅색 알고리즘은 담을 수 있는 물건이 나눌 수 있냐 없냐에 따라 나눈다.
담을 수 있는 물건이 나누어 질 때(설탕 몇 g 등): 분할가능 배낭문제(Fractional Knapsack Problem)
담을 수 있는 물건이 나누어 질 수 없을 때(담는다 or 안담는다): 0-1 배낭문제(0-1Knapsack Problem)
해당 문제는 0-1 배낭문제의 경우다.
이 문제는 다음과 같은 알고리즘으로 풀 수 있다. 풀어서 한 번, 식으로 한 번 설명하겠다.
알고리즘
1) x축엔 가방 1~K 까지의 무게, y축은 물건 N개 개수 만큼의 배열을 만들어준다.
2) 행을 차례대로 돌며 다음과 같은 알고리즘을 수행해준다.
3-0) 현재 물건이 현재 돌고있는 무게보다 작다면 바로 [이전 물건][같은 무게] (knapsack[i-1][j]를 입력해준다.
3-1) 현재 물건을 넣어준다. 물건을 넣은 뒤의 남은 무게를 채울 수 있는 최댓값(knapsack[i-1][j-weight]을 위의 행에서 가져와 더해준다.
3-2) 현재 물건을 넣어주는 것보다. 다른 물건들로 채우는 값(knapsack[i-1][j])을 가져온다.
4) 3-1과 3-2 중 더 큰 값을 knapsack[i][j]에 저장해준다. 이 값은 현재까지의 물건들로 구성할 수 있는 가장 가치 높은 구성이다.
5) knapsack[N][K]는 곧, K무게일 때의 최댓값을 가리킨다.
수식
결국 수식으로 표현하면 다음과 같다.
knapsack[i][j] = max(현재 물건 가치 + knapsack[이전 물건][현재 가방 무게 - 현재 물건 무게], knapsack[이전 물건][현재 가방 무게])
knapsack[i][j] = max(value + knapsack[i - 1][j - weight], knapsack[i - 1][j])
결국 아래와 같은 엑셀이 만들어진다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| weight | value | ||||||||
| 6 | 13 | 0 | 0 | 0 | 0 | 0 | 13 | 13 | |
| 4 | 8 | 0 | 0 | 0 | 8 | 8 | 13 | 13 | |
| 3 | 6 | 0 | 0 | 6 | 8 | 8 | 13 | 14 | |
| 5 | 12 | 0 | 0 | 6 | 8 | 12 | 13 | 14 |
import sys
N, K = map(int, input().split())
stuff = [[0,0]]
knapsack = [[0 for _ in range(K + 1)] for _ in range(N + 1)]
for _ in range(N):
stuff.append(list(map(int, input().split())))
#냅색 문제 풀이
for i in range(1, N + 1):
for j in range(1, K + 1):
weight = stuff[i][0]
value = stuff[i][1]
if j < weight:
knapsack[i][j] = knapsack[i - 1][j] #weight보다 작으면 위의 값을 그대로 가져온다
else:
knapsack[i][j] = max(value + knapsack[i - 1][j - weight], knapsack[i - 1][j])
print(knapsack[N][K])
'Programming [Python] > 백준 알고리즘 솔루션' 카테고리의 다른 글
| #161 백준 파이썬 [1541] 잃어버린 괄호 (0) | 2019.10.31 |
|---|---|
| #160 백준 파이썬 [1931] 회의실배정 - 그리디 알고리즘 (0) | 2019.10.31 |
| #158 백준 파이썬 [9251] LCS (0) | 2019.10.28 |
| #157 백준 파이썬 [2565] 전깃줄 - LIS (1) | 2019.10.28 |
| #156 백준 파이썬 [11054] 가장 긴 바이토닉 부분 수열 - LIS (0) | 2019.10.28 |



